-
Проекції прямої
Пряму в нарисній геометрії розглядають як множину точок, її проекції в загальному випадку також прямі. У системі площин П1 та П2 пряма загального положення зображається двома проекціями. Оскільки дві точки визначають будь-яку пряму, то при розв'язуванні практичних задач, пряму часто задають відрізком.
По відношенню до площин проекцій пряма може займати загальне або часткове положення.
Пряма, яка не паралельна жодній з площин проекцій, називається прямою загального положення.
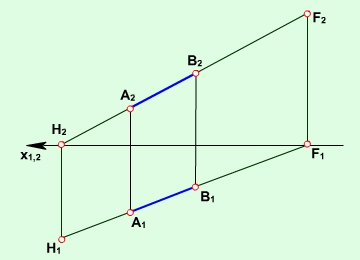
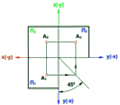
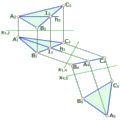
Точки перетину прямої з площинами проекцій називають слідами прямої.
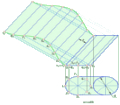
На рис. 2.1.1 зображено епюр прямої та послідовність знаходження її слідів.
Рис. 2.1.1
Прямі часткового або окремого положення – це прямі, які паралельні або перпендикулярні до площин проекцій.
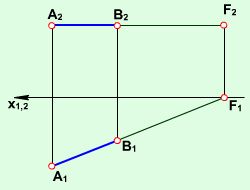
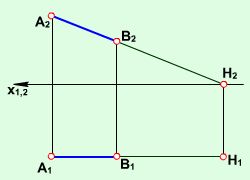
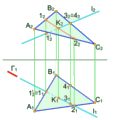
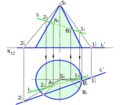
Прямі, паралельні до площин проекцій, належать до так званих прямих рівня і називаються: горизонтальною (рис. 2.1.2), фронтальною (рис. 2.1.3) та профільною прямими (рис. 2.1.4). Відрізки прямих зображуються в натуральну величину на тих площинах проекцій до яких вони паралельні.
Рис. 2.1.2
Рис. 2.1.3
Рис. 2.1.4
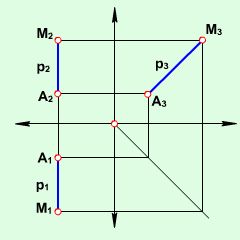
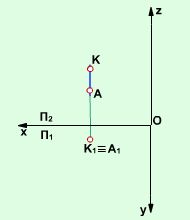
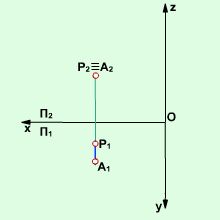
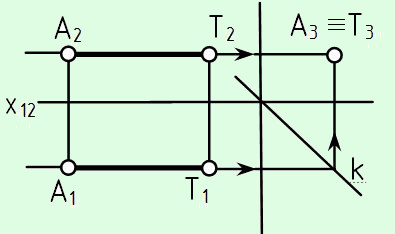
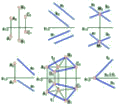
Прямі, перпендикулярні до площин проекцій, називаються проекціюючими (рис. 2.1.5, 2.1.6): АК – горизонтально-проекціююча або вертикальна (рис. 2.1.5), АР – фронтально-проекціююча (рис. 2.1.6), АТ – профільно-проекціююча (рис. 2.1.7). Такі прямі зображуються точкою на площині проекцій, до якої вони перпендикулярні. При цьому вони паралельні двом іншим площинам проекцій.
Рис. 2.1.5
Рис. 2.1.6
Рис. 2.1.7
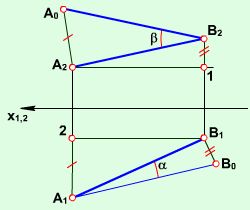
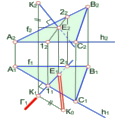
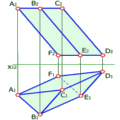
При розгляді відрізка прямої часто виникає потреба у визначенні його натуральної величини та кутів нахилу до площин проекцій П1 та П2, тобто доводиться розв’язувати першу основну метричну задачу. Дійсно, відстань між двома фігурами вимірюється відстанню між найближчими точками цих фігур. Для визначення натуральної величини відрізка прямої загального положення (рис. 2.1.8) використовують метод прямокутного трикутника.
Рис. 2.1.8
Якщо з точки А2 провести промінь, паралельний до осі проекцій х12, а з точки В2 – перпендикулярний до осі х12, то на перетині отримаємо точку 1. Побудувавши перпендикуляр В1В0 до проекції відрізка А1В1 довжиною рівною В21, отримаємо прямокутний трикутник А1В1В0 в якому гіпотенуза А1В0 буде натуральною величиною відрізка АВ. Одночасно визначається і кут α нахилу прямої до горизонтальної площини проекції П1. Щоб знайти кут нахилу прямої до фронтальної площини проекцій, аналогічну побудову треба виконати на полі П2.
Запитання для самоперевірки
- Класифікація прямих в залежності від їх положення відносно площин проекцій.
- Визначення метричних характеристик (натуральної величини, кутів нахилу до площин проекцій) відрізка прямої загального положення методом прямокутного трикутника.
- Способи задання площини в просторі та на епюрі.
- Класифікація площин за їх положенням відносно площин проекцій.